Số thực là một khái niệm quan trọng trong toán học, đóng vai trò nền tảng trong nhiều lĩnh vực khoa học và ứng dụng thực tiễn. Vậy số thực là gì? Ký hiệu của số thực ra sao? Số 0 có phải là số thực không? Và những số nào được xem là số thực? Bài viết này sẽ giúp bạn hiểu rõ hơn về tập hợp số này.

1. Số Thực Là Gì?

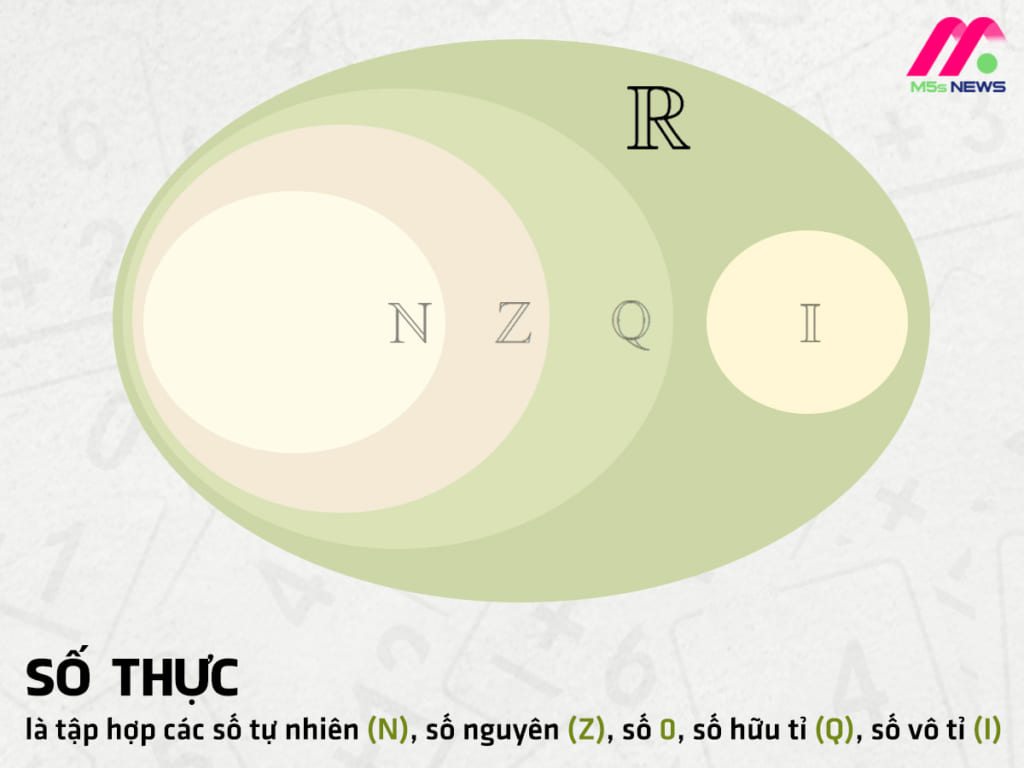
Số thực (Real Numbers) là tập hợp bao gồm tất cả các số có thể biểu diễn trên trục số, bao gồm số hữu tỉ và số vô tỉ. Nói cách khác, số thực là tập hợp các số có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn hoặc tuần hoàn.

Số thực bao gồm:

Số nguyên: …, -3, -2, -1, 0, 1, 2, 3,…
Số hữu tỉ: Các số có thể biểu diễn dưới dạng phân số ab\frac{a}{b}ba với a,ba, ba,b là số nguyên và b≠0b \neq 0b=0. Ví dụ: 1/2, -3/4, 5,…Tập số hữu tỉ ký hiệu là Q
Số vô tỉ: Các số không thể biểu diễn dưới dạng phân số, có số thập phân vô hạn không tuần hoàn. Ví dụ: π\piπ (3.14159…), 2\sqrt{2}2 (1.414…) Tập số vô tỉ được ký hiệu là I

Tập số thực $\mathbb{R}$ phủ kín trục số. $\mathbb{R = Q \cup}I$

2. Số Thực Ký Hiệu Là Gì?

Trong toán học, số thực được ký hiệu là R\mathbb{R}R.

Ký hiệu này xuất phát từ chữ “Real” trong tiếng Anh, có nghĩa là “thực tế”, nhằm phân biệt với số phức C\mathbb{C}C (Complex Numbers).

Trục số thực

Mỗi số thực được biểu diễn bởi một điểm trên trục số.

Đọc thêm: Số nguyên tố là gì? Bảng số nguyên tố trong toán học

Ngược lại mỗi điểm trên trục số đều biểu diễn một số thực.
Chỉ có tập hợp số thực mới lấp đầy trục số.

So sánh các số thực

Phương Pháp

Với hai số thực bất kỳ xxx và yyy, luôn có một trong ba trường hợp xảy ra: x=yx = yx=y, x<yx < yx<y hoặc x>yx > yx>y.
Các số thực lớn hơn 0 được gọi là số thực dương, trong khi các số thực nhỏ hơn 0 được gọi là số thực âm. Số 0 không thuộc cả hai nhóm này.
Việc so sánh các số thực dương được thực hiện tương tự như cách so sánh số hữu tỉ.
Nếu aaa và bbb là hai số thực dương và a>ba > ba>b, thì a>b\sqrt{a} > \sqrt{b}a>b.

Tính chất của tập số thực

Trong tập hợp , ta cũng định nghĩa các phép toán cộng trừ, nhân, chia, lũy thừa, căn bậc…Và trong các phép toán các số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.

Trong tập hợp các số thực, các phép tính có các tính chất đối với phép nhân như sau:

Với mọi $a, b, c$ thuộc $\mathbb{R}$ :
Cộng với số 0: $a + 0 = a$
Tính chất giao hoán: $a + b = b + a$ ;
Tính chất kết hợp: $(a + b) + c = a + (b + c)$
Tính chất giao hoán: a. b = b. a
Tính chất kết hợp: (a. b). c = a. (b. c)
Tính chất nhân với số 1: $a. 1 = 1. a = a$
Tính chất phân phối của phép nhân đối với phép cộng: a. (b + c) = a. b + a. c
Với mỗi số thực a ≠ 0, có số nghịch đảo $\frac{1}{a}$ sao cho $\frac{1}{a}.a = 1$

– Tức là với các phép tính trên cũng có các tính chất giao hoán, kết hợp như trên các tập số khác. Và điều đó tương tự với các phép trừ, nhân, chia…

Đọc thêm: Bảng Cộng Trừ Lớp 2 Và Các Bài Tập Vận Dụng

Mối quan hệ giữa các tập số: $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$

Giá trị tuyệt đối của một số thực

Định nghĩa: Khoảng cách từ điểm a đến điểm 0 trên trục số là giá trị tuyệt đối của một số a (a là số thực). Giá trị tuyệt đối của số không âm là chính nó, giá trị tuyệt đối của số âm là số đối của nó.

Tổng quát:

Nếu $a \geq 0 \Rightarrow |a| = a$
Nếu $a < 0 \Rightarrow |a| = - a$
Nếu $x - a \geq 0 \Rightarrow |x - a| = x - a$
Nếu $x - a \leq 0 \Rightarrow |x - a| = a - x$

Tính chất

Giá trị tuyệt đối của mọi số đều không âm
Tổng quát: $|a| \geq 0$ với mọi a ∈ R

Cụ thể:

Một vài tính chất

– Hai số bằng nhau hoặc đối nhau thì có giá trị tuyệt đối bằng nhau, và ngược lại hai số có giá trị tuyệt đối bằng nhau thì chúng là hai số bằng nhau hoặc đối nhau.

Một vài tính chất

Tổng quát: $|a| = |b| \Leftrightarrow \left\lbrack \begin{matrix} a = b \\ a = - b \\ \end{matrix} \right.$

– Mọi số đều lớn hơn hoặc bằng đối của giá trị tuyệt đối của nó và đồng thời nhỏ hơn hoặc bằng giá trị tuyệt đối của nó.

Tổng quát: $- |a| \leq a \leq |a|$ và $|a| = - a \Leftrightarrow a \leq 0;a = |a| \Leftrightarrow a \geq 0$

– Trong hai số âm số nào nhỏ hơn thì có giá trị tuyệt đối lớn hơn

Tổng quát: Nếu $a < b < 0 \Rightarrow |a| > |b|$

– Trong hai số dương số nào nhỏ hơn thì có giá trị tuyệt đối nhỏ hơn

Tổng quát: Nếu $0 < a < b \Rightarrow |a| < |b|$

– Giá trị tuyệt đối của một tích bằng tích các giá trị tuyệt đối.

Đọc thêm: Tập Hợp Z Là Gì? Ký Hiệu Và Mối quan hệ với tập số #

Tổng quát: $|a.b| = |a|.|b|$

– Giá trị tuyệt đối của một thương bằng thương hai giá trị tuyệt đối.

Tổng quát: $\left| \frac{a}{b} \right| = \frac{|a|}{|b|}$

3. Số 0 Có Phải Là Số Thực Không?

Câu trả lời là CÓ.

Số 0 thuộc tập hợp số nguyên, số hữu tỉ và cũng thuộc tập hợp số thực. Nó là một số đặc biệt trong toán học vì là số trung tâm trên trục số và không thuộc nhóm số âm hay số dương.

4. Số Thực Bao Gồm Những Số Nào?

Số thực bao gồm:

Số dương: 1, 2, 3, 4.5, 7/8, π\piπ, 3\sqrt{3}3…
Số âm: -1, -2.5, -3/4, -5\sqrt{5}5…
Số nguyên: …, -3, -2, -1, 0, 1, 2, 3,…
Số thập phân hữu hạn và vô hạn tuần hoàn: 0.5, 1.25, 0.3333…
Số vô tỉ: π\piπ, eee, 2\sqrt{2}2,…

Tất cả các số có thể biểu diễn trên trục số đều thuộc tập hợp số thực.

Ví Dụ Về Số Thực

Dưới đây là một số ví dụ minh họa về số thực:

Số nguyên: -10, 0, 15
Số hữu tỉ: 3/4, -7/2, 0.25
Số vô tỉ: π\piπ (≈ 3.14159), 2\sqrt{2}2 (≈ 1.414)

Kết Luận

Số thực là một tập hợp quan trọng trong toán học, bao gồm số nguyên, số hữu tỉ và số vô tỉ. Chúng được ký hiệu là R\mathbb{R}R và bao gồm cả số 0. Việc hiểu rõ số thực giúp bạn nắm vững các khái niệm toán học nâng cao và ứng dụng chúng vào thực tế.

Hy vọng bài viết trên đã giúp bạn hiểu rõ hơn về số thực và những đặc điểm của chúng. Nếu bạn có bất kỳ câu hỏi nào, hãy để lại bình luận bên dưới!

Sign up for Newsletter

Toán học

Số Thực Là Gì? Ký Hiệu, Đặc Điểm Và Ví Dụ Minh Họa